Simulations indicate that postmerger gravitational waves from coalescing neutron stars could allow researchers to hear the phase transitions between exotic states of matter.
When you cut yourself, a mass migration begins inside your body: Skin cells flood by the thousands toward the site of the wound, where they will soon lay down fresh layers of protective tissue.
In a new study, researchers from the University of Colorado Boulder have taken an important step toward unraveling the drivers behind this collective behavior. The team has developed an equation learning technique that might one day help scientists grasp how the body rebuilds skin, and could potentially inspire new therapies to accelerate wound healing.
“Learning the rules for how individual cells respond to the proximity and relative motion of other cells is critical to understanding why cells migrate into a wound,” said David Bortz, professor of applied mathematics at CU Boulder and senior author of the new study.
Berkeley Lab scientists have developed new machine learning algorithms to accelerate the analysis of data collected decades ago by HERA, the world’s most powerful electron-proton collider that ran at the DESY national research center in Germany from 1992 to 2007.
Researchers claim to have built a “decoder” algorithm that can reconstruct what somebody is thinking just by monitoring their brain activity using MRI.
Could this be the reason why we haven’t spotted them yet?
Believers in the Drake Equation may have found just the right explanation for why alien civilizations haven’t been spotted by humanity yet. A new study published by U.S.-based researchers states that alien civilizations are likely looking for particular types of stars when trying to establish an intra-galactic base, and our Sun simply does not meet their criterion, Universe Today.
SETI does not make sense
Continue reading “Advanced alien civilizations haven’t contacted us because of the age of our Sun” »
Researchers at the University of Texas at Austin have developed a decoder that uses information from fMRI scans to reconstruct human thoughts. Jerry Tang, Amanda LeBel, Shailee Jain and Alexander Huth have published a paper describing their work on the preprint server bioRxiv.
Prior efforts to create technology that can monitor brain waves and decode them to reconstruct a person’s thoughts have all consisted of probes placed in the brains of willing patients. And while such technology has proven useful for research efforts, it is not practical for use in other applications such as helping people who have lost the ability to speak. In this new effort, the researchers have expanded on work from prior studies by applying findings about reading and interpreting brain waves to data obtained from fMRI scans.
Recognizing that attempting to reconstruct brainwaves into individual words using fMRI was impractical, the researchers designed a decoding device that sought to gain an overall understanding of what was going on in the mind rather than a word-for-word decoding. The decoder they built was a computer algorithm that accepted fMRI data and returned paragraphs describing general thoughts. To train their algorithm, the researchers asked two men and one woman to lie in an fMRI machine while they listened to podcasts and recordings of people telling stories.
Latest News Machine Learning Tech news
Particle physicists have taught algorithms to solve previously unsolvable issues.
Hey everyone! I upgraded a previous redstone build to support 3D Wireframe Rendering! Thanks everyone who suggested this, it was a lot of fun! bigsmile
!!! WATCH PART 1 HERE!!!
https://youtu.be/vfPGuUDuwmo.
Continue reading “I Made a 3D Renderer with just redstone!” »
If you’ve ever played the claw game at an arcade, you know how hard it is to grab and hold onto objects using robotics grippers. Imagine how much more nerve-wracking that game would be if, instead of plush stuffed animals, you were trying to grab a fragile piece of endangered coral or a priceless artifact from a sunken ship.
Most of today’s robotic grippers rely on embedded sensors, complex feedback loops, or advanced machine learning algorithms, combined with the skill of the operator, to grasp fragile or irregularly shaped objects. But researchers from the Harvard John A. Paulson School of Engineering and Applied Sciences (SEAS) have demonstrated an easier way.
Continue reading “Tentacle robot can gently grasp fragile objects” »
Researchers can now predict exactly how soap molecules spread across a body of water, an everyday but surprisingly complex process.
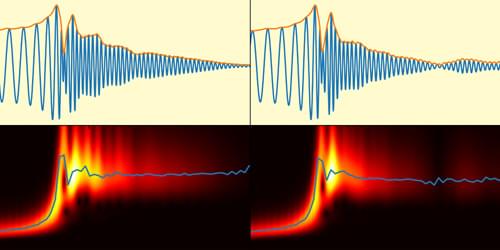
When a tiny drop of soapy water falls onto a pool of liquid, its contents spread out over the pool’s surface. The dynamics of this spreading depend on the local concentration of soap—which varies in time and is difficult to predict—at each point across the entire pool’s surface. Now Thomas Bickel of the University of Bordeaux in Talence, France, and Francois Detcheverry of the University of Lyon, France, have derived an exact time-dependent solution for these distributions [1]. The solution reveals surprisingly rich behaviors in this everyday phenomenon.
The duo considered a surfactant-laden drop spreading over the surface of a deep pool of fluid. Researchers have previously shown that the equations governing the transport of the surfactant particles can be mapped to a partial differential equation known as the Burgers’ equation, which was initially developed to describe flows in turbulent fluids.
