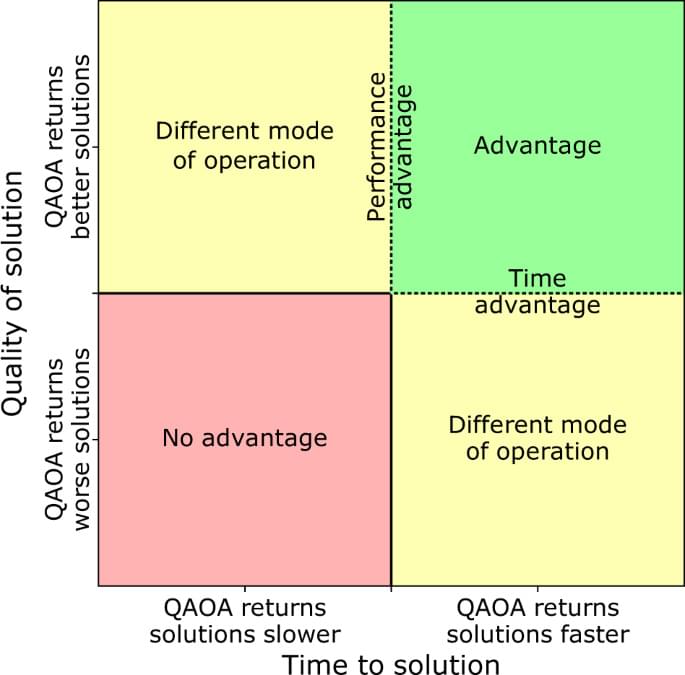
We compare the performance of the Quantum Approximate Optimization Algorithm (QAOA) with state-of-the-art classical solvers Gurobi and MQLib to solve the MaxCut problem on 3-regular graphs. We identify the minimum noiseless sampling frequency and depth p required for a quantum device to outperform classical algorithms. There is potential for quantum advantage on hundreds of qubits and moderate depth with a sampling frequency of 10 kHz. We observe, however, that classical heuristic solvers are capable of producing high-quality approximate solutions in linear time complexity. In order to match this quality for large graph sizes N, a quantum device must support depth p > 11. Additionally, multi-shot QAOA is not efficient on large graphs, indicating that QAOA p ≤ 11 does not scale with N. These results limit achieving quantum advantage for QAOA MaxCut on 3-regular graphs.