“Core season” for the Milky Way has arrived, with our galaxy visible all night as a band of light arching across the sky. Here’s where, when, and how to get the best views in June.



A large impact could have briefly amplified the moon’s weak magnetic field, creating a momentary spike that was recorded in some lunar rocks. Scientists may have solved the mystery of why the moon shows ancient signs of magnetism although it has no magnetic field today. An impact, such as from a large asteroid, could have generated a cloud of ionized particles that briefly enveloped the moon and amplified its weak magnetic field.
Where did the moon’s magnetism go? Scientists have puzzled over this question for decades, ever since orbiting spacecraft picked up signs of a high magnetic field in lunar surface rocks. The moon itself has no inherent magnetism today.
Now, MIT scientists may have solved the mystery. They propose that a combination of an ancient, weak magnetic field and a large, plasma-generating impact may have temporarily created a strong magnetic field, concentrated on the far side of the moon.



The entire field of mathematics summarised in a single map! This shows how pure mathematics and applied mathematics relate to each other and all of the sub-topics they are made from.
#mathematics #DomainOfScience.
If you would like to buy a poster of this map, they are available here:
North America: https://store.dftba.com/products/map–… else: http://www.redbubble.com/people/domin… French version: https://www.redbubble.com/people/domi… Spanish Version: https://www.redbubble.com/people/domi… I have also made a version available for educational use which you can find here: https://www.flickr.com/photos/9586967… To err is to human, and I human a lot. I always try my best to be as correct as possible, but unfortunately I make mistakes. This is the errata where I correct my silly mistakes. My goal is to one day do a video with no errors! 1. The number one is not a prime number. The definition of a prime number is a number can be divided evenly only by 1, or itself. And it must be a whole number GREATER than 1. (This last bit is the bit I forgot). 2. In the trigonometry section I drew cos(theta) = opposite / adjacent. This is the kind of thing you learn in high school and guess what. I got it wrong! Dummy. It should be cos(theta) = adjacent / hypotenuse. 3. My drawing of dice is slightly wrong. Most dice have their opposite sides adding up to 7, so when I drew 3 and 4 next to each other that is incorrect. 4. I said that the Gödel Incompleteness Theorems implied that mathematics is made up by humans, but that is wrong, just ignore that statement. I have learned more about it now, here is a good video explaining it: • Gödel’s Incompleteness Theorem — Numberphile 5. In the animation about imaginary numbers I drew the real axis as vertical and the imaginary axis as horizontal which is opposite to the conventional way it is done. Thanks so much to my supporters on Patreon. I hope to make money from my videos one day, but I’m not there yet! If you enjoy my videos and would like to help me make more this is the best way and I appreciate it very much.
/ domainofscience Here are links to some of the sources I used in this video. Links: Summary of mathematics: https://en.wikipedia.org/wiki/Mathema… Earliest human counting: http://mathtimeline.weebly.com/early–… First use of zero: https://en.wikipedia.org/wiki/0#History http://www.livescience.com/27853-who–… First use of negative numbers: https://www.quora.com/Who-is-the-inve… Renaissance science: https://en.wikipedia.org/wiki/History… History of complex numbers: http://rossroessler.tripod.com/ https://en.wikipedia.org/wiki/Mathema… Proof that pi is irrational: https://www.quora.com/How-do-you-prov… and https://en.wikipedia.org/wiki/Proof_t… Also, if you enjoyed this video, you will probably like my science books, available in all good books shops around the work and is printed in 16 languages. Links are below or just search for Professor Astro Cat. They are fun children’s books aimed at the age range 7–12. But they are also a hit with adults who want good explanations of science. The books have won awards and the app won a Webby. Frontiers of Space: http://nobrow.net/shop/professor-astr… Atomic Adventure: http://nobrow.net/shop/professor-astr… Intergalactic Activity Book: http://nobrow.net/shop/professor-astr… Solar System App: Find me on twitter, instagram, and my website: http://dominicwalliman.com
/ dominicwalliman
/ dominicwalliman
/ dominicwalliman.
Everywhere else: http://www.redbubble.com/people/domin…
French version: https://www.redbubble.com/people/domi…
Spanish Version: https://www.redbubble.com/people/domi…
I have also made a version available for educational use which you can find here: https://www.flickr.com/photos/9586967…
To err is to human, and I human a lot. I always try my best to be as correct as possible, but unfortunately I make mistakes. This is the errata where I correct my silly mistakes. My goal is to one day do a video with no errors!
1. The number one is not a prime number. The definition of a prime number is a number can be divided evenly only by 1, or itself. And it must be a whole number GREATER than 1. (This last bit is the bit I forgot).

A group of astronomers from across the globe, including a team from the University of Washington and led by Queen’s University Belfast, have revealed new research showing that millions of new solar system objects will be detected by a brand-new facility, which is expected to come online later in 2025.
The NSF–DOE Vera C. Rubin Observatory is set to revolutionize our knowledge of the solar system’s “small bodies”—asteroids, comets and other minor planets.
The Rubin Observatory, under construction on the Cerro Pachón ridge in northern Chile, features the 8.4-meter Simonyi Survey Telescope with a unique three-mirror design capable of surveying the entire visible sky every few nights.

We know dinosaurs were around 99 million years ago, but now new research has identified a kind of parasitic wasp that was flying around back then (and which has a strange way of catching its prey).
The species now called Sirenobethylus charybdis had a bizarre mechanism that worked like a Venus flytrap which caught the prey, and then the wasps impregnated them with their eggs, researchers noted in the journal BMC Biology.

For years, astronomers have predicted a dramatic fate for our galaxy: a head-on collision with Andromeda, our nearest large galactic neighbor. This merger—expected in about 5 billion years—has become a staple of astronomy documentaries, textbooks and popular science writing.
But in our new study published in Nature Astronomy, led by Till Sawala from the University of Helsinki, we find the Milky Way’s future might not be as certain previously assumed.
By carefully accounting for uncertainties in existing measurements, and including the gravitational influence of other nearby galaxies, we found there is only about a 50% chance the Milky Way and Andromeda will merge in the next 10 billion years.
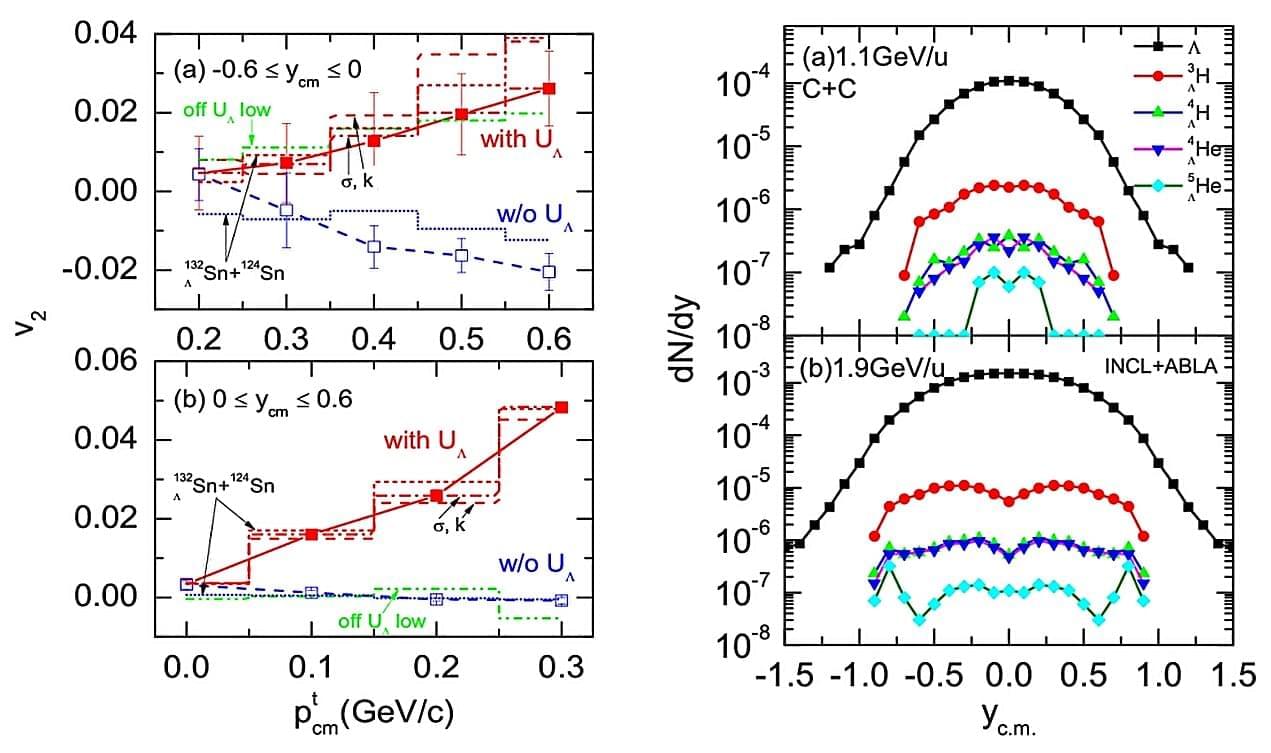
A research team led by Prof. Yong Gaochan from the Institute of Modern Physics (IMP) of the Chinese Academy of Sciences has proposed a novel experimental method to probe the hyperon potential, offering new insights into resolving the longstanding “hyperon puzzle” in neutron stars. These findings were published in Physics Letters B and Physical Review C.
According to conventional theories, the extreme densities within neutron stars lead to the production of hyperons containing strange quarks (e.g., Λ particles). These hyperons significantly soften the equation of state (EoS) and reduce the maximum mass of neutron stars. However, astronomical observations have discovered neutron stars with masses approaching or even exceeding twice that of the sun, contradicting theoretical predictions.
Hyperon potential refers to the interaction potential between a hyperon and a nucleon. Aiming to resolve the “neutron star hyperon puzzle,” the study of hyperon potential has emerged as a frontier topic in the interdisciplinary field of nuclear and astrophysics. Currently, it is believed that if hyperon potentials exhibit stronger repulsion at high densities, they could counteract the softening effect of the EoS, thereby allowing massive neutron stars to exist.