Masaki Kashiwara is the first Japanese person to be awarded the most prestigious prize in mathematics.



The DeepSeek-V3-0324, named after its predecessor and the launch date, has “enhanced reasoning capabilities, optimised front-end web development and upgraded Chinese writing proficiency”, according to a notice on the company’s website.
The new version and DeepSeek V3 are both foundation models trained on vast data sets that can be applied in different use cases, including that of a chatbot. DeepSeek R1, the reasoning model, is based on DeepSeek V3.
The updated foundation model has made improvements in several benchmarks, especially the American Invitational Mathematics Examination (AIME), where it scored 59.4 compared with 39.6 for its predecessor, while achieving an increase of 10 points on LiveCodeBench to achieve 49.2, DeepSeek data showed.

Pedestrian crossings generally showcase the best in pedestrian behavior, with people naturally forming orderly lanes as they cross the road, smoothly passing those coming from the opposite direction without any bumps or scrapes. Sometimes, however, the flow gets chaotic, with individuals weaving through the crowd on their own haphazard paths to the other side.
Now, an international team of mathematicians, co-led by Professor Tim Rogers at the University of Bath in the UK and Dr. Karol Bacik at MIT in the US has made an important breakthrough in their understanding of what causes human flows to disintegrate into tangles. This discovery has the potential to help planners design road crossings and other pedestrian spaces that minimize chaos and enhance safety and efficiency.
In a paper appearing in the journal Proceedings of the National Academy of Sciences, the team pinned down the precise point at which crowds of pedestrians crossing a road collapse from order to disorder.
In the ebb and flow of crowded crosswalks, a surprising pattern emerges: people can naturally form neat lanes of movement. But what flips the switch from graceful organization to chaotic weaving?
An international team of researchers has pinpointed a specific tipping point: when pedestrians deviate more than 13 degrees from their path, order collapses. Backed by math, experiments, and real-world testing, this discovery could revolutionize how cities manage foot traffic.
From flow to frenzy: what disrupts pedestrian order?
Joscha Bach is a cognitive scientist focusing on cognitive architectures, consciousness, models of mental representation, emotion, motivation and sociality.
Patreon: / curtjaimungal.
Crypto: https://tinyurl.com/cryptoTOE
PayPal: https://tinyurl.com/paypalTOE
Twitter: / toewithcurt.
Discord Invite: / discord.
iTunes: https://podcasts.apple.com/ca/podcast… https://pdora.co/33b9lfP Spotify: https://open.spotify.com/show/4gL14b9… Subreddit r/TheoriesOfEverything: / theoriesofeverything Merch: https://tinyurl.com/TOEmerch 0:00:00 Introduction 0:00:17 Bach’s work ethic / daily routine 0:01:35 What is your definition of truth? 0:04:41 Nature’s substratum is a “quantum graph”? 0:06:25 Mathematics as the descriptor of all language 0:13:52 Why is constructivist mathematics “real”? What’s the definition of “real”? 0:17:06 What does it mean to “exist”? Does “pi” exist? 0:20:14 The mystery of something vs. nothing. Existence is the default. 0:21:11 Bach’s model vs. the multiverse 0:26:51 Is the universe deterministic 0:28:23 What determines the initial conditions, as well as the rules? 0:30:55 What is time? Is time fundamental? 0:34:21 What’s the optimal algorithm for finding truth? 0:40:40 Are the fundamental laws of physics ultimately “simple”? 0:50:17 The relationship between art and the artist’s cost function 0:54:02 Ideas are stories, being directed by intuitions 0:58:00 Society has a minimal role in training your intuitions 0:59:24 Why does art benefit from a repressive government? 1:04:01 A market case for civil rights 1:06:40 Fascism vs communism 1:10:50 Bach’s “control / attention / reflective recall” model 1:13:32 What’s more fundamental… Consciousness or attention? 1:16:02 The Chinese Room Experiment 1:25:22 Is understanding predicated on consciousness? 1:26:22 Integrated Information Theory of consciousness (IIT) 1:30:15 Donald Hoffman’s theory of consciousness 1:32:40 Douglas Hofstadter’s “strange loop” theory of consciousness 1:34:10 Holonomic Brain theory of consciousness 1:34:42 Daniel Dennett’s theory of consciousness 1:36:57 Sensorimotor theory of consciousness (embodied cognition) 1:44:39 What is intelligence? 1:45:08 Intelligence vs. consciousness 1:46:36 Where does Free Will come into play, in Bach’s model? 1:48:46 The opposite of free will can lead to, or feel like, addiction 1:51:48 Changing your identity to effectively live forever 1:59:13 Depersonalization disorder as a result of conceiving of your “self” as illusory 2:02:25 Dealing with a fear of loss of control 2:05:00 What about heart and conscience? 2:07:28 How to test / falsify Bach’s model of consciousness 2:13:46 How has Bach’s model changed in the past few years? 2:14:41 Why Bach doesn’t practice Lucid Dreaming anymore 2:15:33 Dreams and GAN’s (a machine learning framework) 2:18:08 If dreams are for helping us learn, why don’t we consciously remember our dreams 2:19:58 Are dreams “real”? Is all of reality a dream? 2:20:39 How do you practically change your experience to be most positive / helpful? 2:23:56 What’s more important than survival? What’s worth dying for? 2:28:27 Bach’s identity 2:29:44 Is there anything objectively wrong with hating humanity? 2:30:31 Practical Platonism 2:33:00 What “God” is 2:36:24 Gods are as real as you, Bach claims 2:37:44 What “prayer” is, and why it works 2:41:06 Our society has lost its future and thus our culture 2:43:24 What does Bach disagree with Jordan Peterson about? 2:47:16 The millennials are the first generation that’s authoritarian since WW2 2:48:31 Bach’s views on the “social justice” movement 2:51:29 Universal Basic Income as an answer to social inequality, or General Artificial Intelligence? 2:57:39 Nested hierarchy of “I“s (the conflicts within ourselves) 2:59:22 In the USA, innovation is “cheating” (for the most part) 3:02:27 Activists are usually operating on false information 3:03:04 Bach’s Marxist roots and lessons to his former self 3:08:45 BONUS BIT: On societies problems.
Pandora: https://pdora.co/33b9lfP
Spotify: https://open.spotify.com/show/4gL14b9…
Subreddit r/TheoriesOfEverything: / theoriesofeverything.
Merch: https://tinyurl.com/TOEmerch.
0:00:00 Introduction.
0:00:17 Bach’s work ethic / daily routine.
0:01:35 What is your definition of truth?
0:04:41 Nature’s substratum is a \.

He majored in Mathematical Engineering in 1958 from the University of Tokyo then graduated in 1963 from the Graduate School of the University of Tokyo.
His Master of Engineering in 1960 was entitled Topological and Information-Theoretical Foundation of Diakoptics and Codiakoptics. His Doctor of Engineering in 1963 was entitled Diakoptics of Information Spaces.
Shun’ichi Amari received several awards and is a visiting professor of various universities.

This is the Fourier Transform. You can thank it for providing the music you stream every day, squeezing down the images you see on the Internet into tiny little JPG files, and even powering your noise-canceling headphones. Here’s how it works.
The equation owes its power to the way that it lets mathematicians quickly understand the frequency content of any kind of signal. It’s quite a feat. But don’t just take my word for it—in 1867, the physicist Lord Kelvin expressed his undying love for this fine piece of mathematics, too. He wrote, “Fourier’s theorem is not only one of the most beautiful results of modern analysis, but it may be said to furnish an indispensable instrument in the treatment of nearly every recondite question in modern physics.” And so it remains.
Math Will Tear Us Apart

Somehow, we all know how a warp drive works. You’re in your spaceship and you need to get to another star. So you press a button or flip a switch or pull a lever and your ship just goes fast. Like really fast. Faster than the speed of light. Fast enough that you can get to your next destination by the end of the next commercial break.
Warp drives are staples of science fiction. And in 1994, they became a part of science fact. That’s when Mexican physicist Miguel Alcubierre, who was inspired by Star Trek, decided to see if it was possible to build a warp drive. Not like actually build one with wrenches and pipes, but to see if it was even possible to be allowed to build a warp drive given our current knowledge of physics.
Physics is just a mathematical exploration of the natural universe, and the natural universe appears to play by certain rules. Certain actions are allowed, and other actions are not allowed. And the actions that are allowed have to proceed in a certain orderly fashion. Physics tries to capture all of those rules and express them in mathematical form. So Alcubierre wondered: does our knowledge of how nature works permit a warp drive or not?
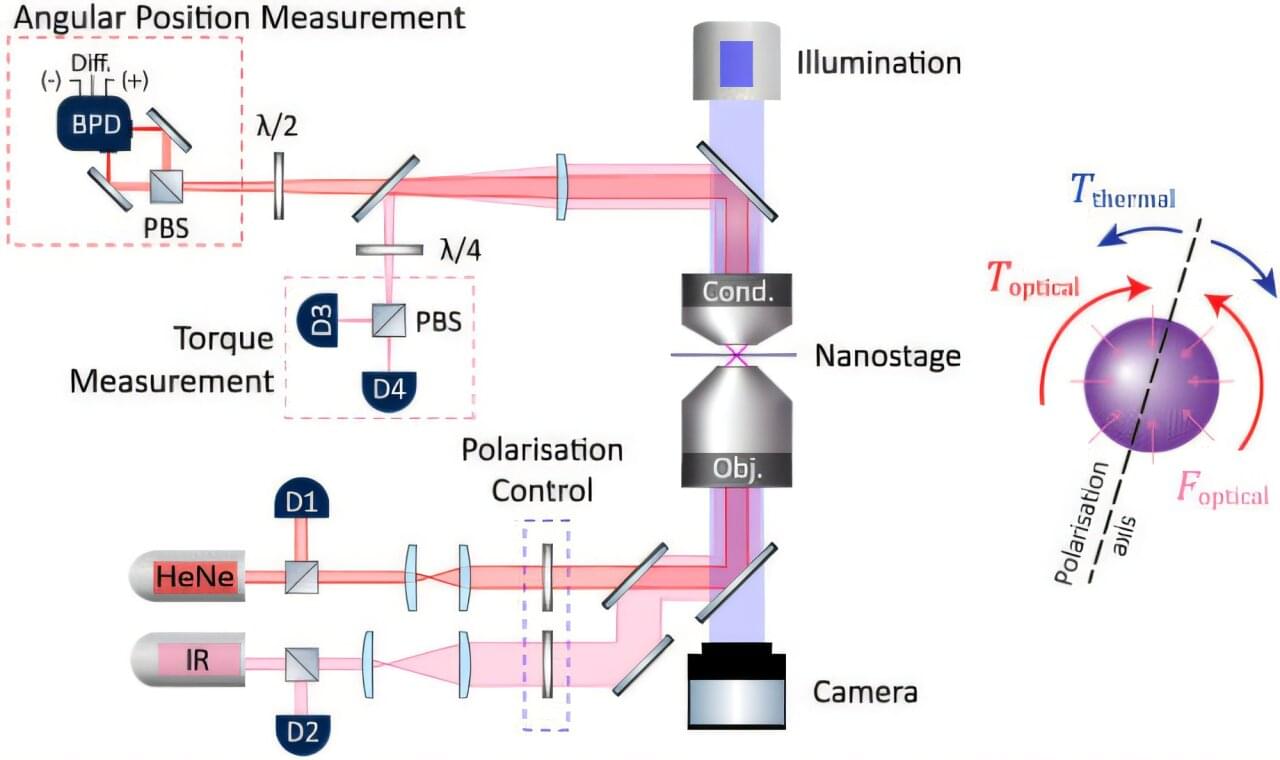
Researchers will soon be able to study biological changes at scales and speeds not previously possible to significantly expand knowledge in areas such as disease progression and drug delivery.
Physicists at The University of Queensland have used “tweezers made from light” to measure activity within microscopic systems over timeframes as short as milliseconds. Professor Halina Rubinsztein-Dunlop from UQ’s School of Mathematics and Physics said the method could help biologists understand what was happening within single living cells.
“For example, they will be able to look at how a cell is dividing, how it responds to outside stimuli, or even how chemical reactions affect cell properties,” Professor Rubinsztein-Dunlop said.