Quantum computers promise to solve some problems exponentially faster than classical computers, but there are only a handful of examples with such a dramatic speedup, such as Shor’s factoring algorithm and quantum simulation. Of those few examples, the majority of them involve simulating physical systems that are inherently quantum mechanical — a natural application for quantum computers. But what about simulating systems that are not inherently quantum? Can quantum computers offer an exponential advantage for this?
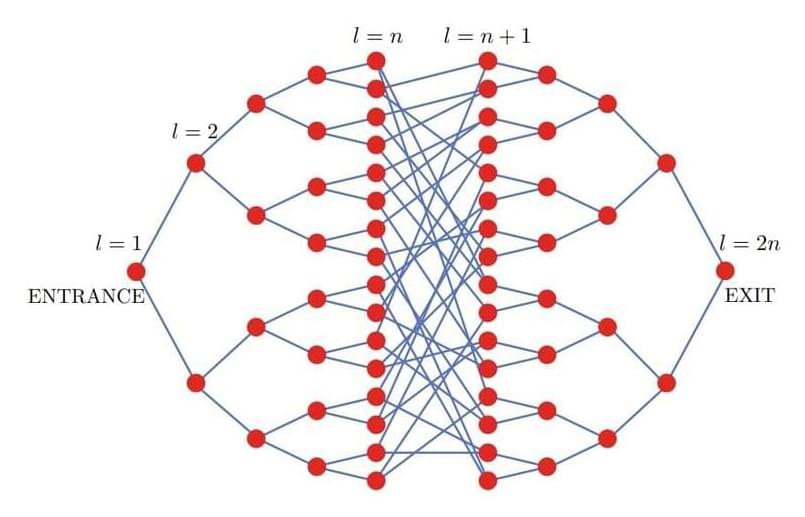
In “Exponential quantum speedup in simulating coupled classical oscillators”, published in Physical Review X (PRX) and presented at the Symposium on Foundations of Computer Science (FOCS 2023), we report on the discovery of a new quantum algorithm that offers an exponential advantage for simulating coupled classical harmonic oscillators. These are some of the most fundamental, ubiquitous systems in nature and can describe the physics of countless natural systems, from electrical circuits to molecular vibrations to the mechanics of bridges. In collaboration with Dominic Berry of Macquarie University and Nathan Wiebe of the University of Toronto, we found a mapping that can transform any system involving coupled oscillators into a problem describing the time evolution of a quantum system. Given certain constraints, this problem can be solved with a quantum computer exponentially faster than it can with a classical computer.